Oumuamua – As Improbably Skinny as the Most Slender Human Skyscrapers
Alien Technology?
A story on the BBC website reports that the interstellar
visitor object, Oumuamua is being examined for signs of alien technology. Billionaire Yuri Milner will be funding a
project, making use of the Green Bank Radio Telescope in West Virginia, to
listen for any signals (intentional or not) that would indicate a non-natural
source. That might include actual attempts at communication, or radio signals
that leak from the object unintentionally, say from some type of electrical
machinery. Even an unexplained heat
signature would be of interest.
It seems like a real long shot, but then the term “long” is
very apt for this object, as it is very unusual for its long shape, about a 10
to 1 ratio of long axis to short axis.
Estimating Oumuamua’s Size and Shape
Contrary to what one might expect based on pictures in the
media, we haven’t actually been able to photograph it in the glorious detail
generally shown, as above. Those are
artist renderings. In fact we haven’t
really been able to photograph it at all, as far as its shape is
concerned. From the distance at which we
have observed it, it is just a speck of light, albeit a speck that varies in
brightness.
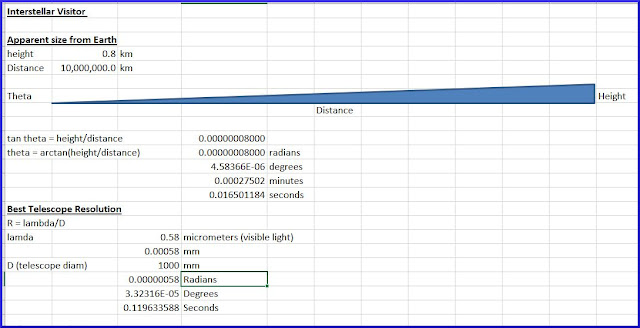
Why don’t we have nice photos? Basically, it is too small. It is thought to be about 800 meters long, by
80 meters wide, by 80 meters deep. A
little trigonometry shows that an 0.8 km object would subtend an angle of about
0.016 arc seconds, even at the relatively close distance of 10,000,000 km.
The telescopes and cameras that were used to
photograph Oumuamua had a resolution, at best, of only about 0.1 arc seconds
per pixel, so it can’t really be seen as an extended object, at the distances
at which it has been observed (it was at roughly Mars-like distances when first
observed, as indicated in the picture taken from the Nature paper).
The reason that the object is thought to have this shape is
due to its light curve. Oumuamua varies in how bright it is by about 2.5
magnitudes over about 8 hours, which is equivalent to a brightness change of
about 10 times, as explained below:
- The magnitude scale is constructed so that a difference of 5 magnitudes equals a difference of 100 time in intrinsic magnitude. Another way of looking at that, is that each magnitude change represents about 2.5 times change in brightness.
- So, 5 magnitudes is about 2.5 raised to the fifth power, which is about 98. A difference of 2.5 magnitudes is about 2.5 railed to the power 2.5, which is 9.88, or nearly 10.
- Note that I am making some approximations here, but they are close enough for the purpose, given the uncertainties in observational data, anyway.
The most likely reason for this change in brightness is that
it is that Oumuamua is rotating every 8 hours, with its short profile facing
Earth when it is dimmest and its long profile facing Earth when it is brightest
(like a North American football tumbling end over end after a kick-off, as
observed from the kicker’s point of view). So, the difference of a factor of 10
in brightness would be due to the change in the amount of surface area facing
the Earth, and thus the amount of reflecting surface that is reflecting
sunlight back to us.
An Underestimate of the Elongation?
On interesting aspect of this explanation, is that the 10 to
1 elongation estimate might well be a significant underestimate, depending on
the angle of Oumuamua’s rotation plane, as seen from the Earth.
I mocked up a model of the interstellar asteroid, with
approximately the same ratio of dimensions as Oumuamua. This was a piece of scrap wood with
dimensions of about 15 inches by 1.50 inches by 1.75 inches. That’s pretty close to the 10 to 1 elongation
of Oumuamua.
I then mounted this on a tripod, using some good old duct
tape. The tripod could be rotated in all
three dimensions. That was then placed
next to a wall with a light source across the room. This was meant to very roughly model the
situation of the asteroid, relative to the Earth, with the size of the shadow
on the wall corresponding to the amount of area that the asteroid would present
to the sun, and thereby the amount of light being reflected back to an observer
on Earth.
This exercise is also a straightforward example of
projecting a 3-D object onto a 2-D surface (more trigonometry), but a picture
is worth a thousand words, so I thought this would be interesting an persuasive
in illustrating the mathematical situation.
I have named this the “propeller” in the images below. One can think of how a spinning propeller
would look to an observer, at various angles.
Remember, though, that the propeller is rotating very slowly, about once
every 8 hours, so the apparent size of it can be easily measured at various
stages in the rotation. Note also, that
the pictures had to be taken at a bit of an angle, otherwise there would be no
shadow to measure, since the photographer would block the light (“shades” of
the observer affecting the observation).
So, the photos are a bit distorted, relative to the shadow measurements
actually taken with a tape measure.
Case 1 is the situation that is yields the maximum ratio of
length to width/depth. When the asteroid
model is pointing straight up and down, relative to the observer, its
shadow measures about 17 inches long by
1.75 inches wide (the shadow is a bit longer than the model, because the light
source is a non-spherical light bulb about 10 feet away, so there are some
complicated penumbra effects). When it
is pointing sideways, relative to the observer, it measures about 1.75 inches
long by 1.75 inches wide. So, that
yields an elongation of about 10, which is the elongation estimated for Oumuamua
in the reports.
Case 2 is the situation that is yields the minimum ratio of
length to width/depth, which is to say no elongation at all. When the asteroid model is pointing straight
up and down, relative to the observer, its shadow measures about 16 inches long by 1.75 inches
wide. When it is pointing sideways,
relative to the observer, it measures about the same. So, that yields an elongation of about 1, or
no elongation at all. So, if a long
object (but relatively small) was to fly away from us, spinning like a
propeller face on, we wouldn’t really know anything about its shape, as it
would seem equally bright throughout its rotation.
Case 3 is an intermediate situation, with the plane of the
propeller at about 45 degrees to the observers line of sight. When the asteroid model is pointing straight
up and down, relative to the observer, its shadow measures about 16.5 inches
long by 2.25 inches wide. When it is
pointing sideways, relative to the observer, it measures about 13.5 inches long
by 1.75 inches wide. So, that yields an
elongation of well under 2, or not much at all, event thought we know that the
dimensions of the object are actually 10 to 1.
So, for such an object oriented at an oblique angle, we would be
seriously misled about its real size.
The same is true for other oblique angles – even an object inclined only
30 degrees from straight-on yields a fairly small apparent elongation, on the
order of 2.
Of course, if one followed the object for quite a long time
through its orbit, its orientation relative to the Earth would constantly
shift, so that would provide extra information.
But, in practice, it would become difficult to see at all, as it
continued in its orbit. Here’s a quote
in the Nature discovery paper:
“The inset shows the inner solar
system, with the solid line segment along ‘Oumuamua’s trajectory indicating the
short window of two weeks during which it was bright enough (median magnitude
of light curve V~20-24) to be studied by large telescopes on Earth.”
I should note that an early version of the Astrophysical Journal paper alludes to this issue noting that the “axis ratio is a lower limit because of the effects of projection, and is extreme relative to most asteroids”.
Even a 10 to 1 ratio is surprisingly elongated. In fact, skyscrapers with that elongation are considered to be very slender structures, as is described in the skyscraper.org website:
WHAT IS
SLENDERNESS?
"Slenderness" is an engineering
definition. Structural engineers generally consider skyscrapers with a minimum
1:10 or 1:12 ratio (of the width of the building's base to its height) to be
"slender." Slenderness is a proportion based on the width of the base
to the height of the building.
The World Trade Center North Tower was the
tallest building in the world on its completion in 1971. But at a height of
1,368 feet and with a big square floor plate, 209 feet on each side, the ratio
of its base to height was less than 1:7. This image compares at the same scale
the former 1 WTC and the residential tower 432 Park Avenue, now under
construction. The base of the apartment building is 93 feet square, and the
shaft will rise to 1,396 feet, making its slenderness ratio 1:15. To visualize
a 1:12 ratio, we show a ruler 1-inch wide and set on end. The eighteen towers
on our chart range from a ratio of 1:10 to an extraordinary 1:23 at 111 W. 57
Street.
Here’s a photo of the Empire State Building, in New York
(which is not considered a slender building).
It has an elongation of perhaps 7 or 8 to 1, based on floor space,
number of stories, and overall height.
It is hard to find a natural rock formation on Earth that
comes anywhere near a 10 to 1 elongation.
Here’s the well-known Chimney Rock, in the U.S.A. (Nebraska). It only looks to be about 4 to 1 elongation,
on average, considering just the top spire.
So, if you observed Oumuamua from a spaceship, very close up
(like the recent ESA mission to the comet), its shape might remind you of a
skyscraper, and possibly an extremely skinny one (though if it looked too much like the Empire State Building, you might be running short of oxygen). As far as we know, there is nothing like it
in our solar system.
The question is, what process made such an unusual object
(see my earlier Oumuamua blog for more on that). I guess that’s the question on Russian
billionaire Yuri Milner’s mind as well.
Sources:
Nature letter
doi:10.1038/nature25020
A brief visit from a red and
extremely elongated interstellar asteroid
Karen J. Meech, Robert Weryk,
Marco Micheli, Jan T. Kleyna, Olivier R. Hainaut, Robert Jedicke, Richard J.
Wainscoat,Kenneth C. Chambers, Jacqueline V. Keane, Andreea Petric, Larry
Denneau, Eugene Magnier, Travis Berger, Mark E. Huber, Heather Flewelling,
Chris Waters, Eva Schunova-Lilly & Serge Chastel
Google Images
---------------------------------------------------------------------------------------------------------------------
Now that you
have read about a real interstellar interloper (natural or not), you should
consider reading some Science Fiction.
How about a short story, also about interstellar interlopers. It also features one possible scenario to
explain why we haven’t met ET yet (as far as we know, anyway). Only 99 cents on Amazon.
Oh, and it
has dogs. Everyone loves dogs, don’t
they?
The Zoo Hypothesis or The News of the World: A Science Fiction Story
In the field known as Astrobiology, there is a research
program called SETI, The Search for Extraterrestrial Intelligence. At the heart of SETI, there is a mystery
known as The Great Silence, or The Fermi Paradox, named after the famous
physicist Enrico Fermi. Essentially, he
asked “If they exist, where are they?”.
Some quite cogent arguments maintain that if there was
extraterrestrial intelligence, they should have visited the Earth by now. This
story, a bit tongue in cheek, gives a fictional account of one explanation for
The Great Silence, known as The Zoo Hypothesis.
Are we a protected species, in a Cosmic Zoo? If so, how did this come about? Read on, for one possible solution to The
Fermi Paradox.
The short story is about 6300 words, or about half an hour
at typical reading speeds. It will set you back 99 cents, unless it is free, which it occasionally is.
https://www.amazon.com/dp/B076RR1PGD
https://www.amazon.co.uk/dp/B076RR1PGD
https://www.amazon.ca/dp/B076RR1PGD
https://www.amazon.com/dp/B076RR1PGD
https://www.amazon.co.uk/dp/B076RR1PGD
https://www.amazon.ca/dp/B076RR1PGD











No comments:
Post a Comment